第三章

3.1贝叶斯决策与MAP分类器

  • 当两个类有相同的均值时，MICD分类器倾向于选择方差更大的类，但其实决策真值应该倾向于方差更小，即分布更紧致的类。感觉有点像同心圆，有相同的圆心，然后每一圈之间代表一个类。
  • 基于距离的决策一般只考虑了训练样本的分布情况，忽略了类与类之间的关系。
  • 先验概率：根据以往的经验和分析得到的概率，不依靠观测数据。
  • 观测似然概率：也叫似然概率，这个可以比做成在很多组参数中，选择一组最能拟合观测数据的参数。
  • MAP分类器，就是选择后验概率最大的那个类，决策边界也就是两个后验概率相等的地方。一般单维空间，有条决策边界，高维空间，就是非线性的边界了。
  • 决策误差，就是与真值相比，分类分错了的误差，以二分类来说，概率误差就是等于未选择的另一个类的后验概率。
  • 平均概率误差就是样本的概率误差的均值。
  • MAP分类器选择后验概率最大的类，也就是在最小化平均概率误差，也就是在最小化决策误差。

3.2MAP分类器：高斯观测概率

  • 先验概率和观测概率可以有常数表达、参数化解析表达（高斯分布等）、非参数化表达（直方图、核密度等）。
  • 高斯分布带入MAP分类器，对于二分类问题，如果两个类的方差，即标准差相等，决策边界就只有一条，因为二次项消除了。此时，如果类1的均值小于类2的均值，那么类1在分类时就比较吃亏了，因为决策边界会偏向类1，也就是说属于类1的X轴所对应区域减小，分类器偏向类2，也就是偏向先验概率高的类。
  • 同样是高斯分布，二分类问题，如果方差不相等，将会有两条决策边界，也就是非线性的边界了，此时如果类1的标准差小于类2的标准差，并且两个类均值相等，那么类2就吃亏了，分类器会偏向标准差小的类，也就是更瘦、更紧致的类。因为当两个后验概率相等时，在当前条件下，减去的常数项大于0，也就是方程解出的两个解的绝对距离会加大，导致属于类1的X轴区域加大，分类器偏向类1。

3.3决策风险与贝叶斯分类器

  • 由于数据集不平衡等其他原因，引出了决策风险和损失，来控制MAP分类器。因此贝叶斯分类器=MAP分类器+决策风险。
  • 贝叶斯分类选择决策风险最小的类。
  • 加入了决策风险后，使得样本个数少的类对应X轴区域加大，缓解了一边倒的趋势。
  • 贝叶斯决策的期望损失根据公式，用通俗的话来说就是所有样本，对于所有的类的后验概率乘对应的损失值的和。
  • 因此贝叶斯分类器要做的事就是去最小化期望损失。
  • 但是这时候又有问题，如果特征维度较高，那么特征与特征之间的相关性会导致似然概率非常难计算，也就导致了后验概率非常难计算。
  • 所以这时候就引出了朴素贝叶斯分类器，它假设了每个特征之间是相互独立的，也就解决了上面的问题。
  • 对于拒绝选项，也就是虽然选出了最大后验概率对应的类，但是这个最大后验概率也很小，比如在决策边界附近，不太能接受，那就设置个阈值，拒绝他。这样可以提高分类器的各项指标，F1-Score等等。比如对于医疗方面的应用，可以把这些拒绝的样本让专家去判断。

3.4最大似然估计

  • 在上面的贝叶斯分类器中，需要事先知道先验概率和似然概率才能求后验概率，但先验概率和似然概率并不是一开始就知道的，提供的数据集只是冷冰冰的数字，因此就需要使用相关算法从这些数字中得到先验概率和似然概率。
  • 此时有两种参数估计方法，最大似然估计和贝叶斯估计。
  • 最大似然估计就是想要找到一些参数，能够最大化地去拟合我们地数据分布。当然，不能把所以数据都拿来进行计算，这样计算量非常大，所以需要进行采样，并假设了采样的样本都符合相互独立条件。
  • 似然函数的目标函数就是希望在给定参数（但这里的参数并不是最优值）的条件下，求每个样本似然概率乘积的最大值。
  • 既然要求最大值，那就需要进行求偏导了，令偏导等于0。
  • 因此可以得到先验概率的最大似然估计就是该类训练样本出现的频率。
  • 接着我们假设我们的样本数据服从高斯分布，那么我们就需要去学习均值和方差，或者协方差。
  • 同样的，要求似然函数的目标函数的最大值，并求偏导，所以要将高斯分布的表达式代入似然函数。
  • 求完之后，可以得到高斯分布的均值的最大似然估计等于所有训练样本的均值，协方差的最大似然估计等于所有训练样本的协方差。

3.5最大似然的估计偏差

  • 既然是估计，那就可能会有偏差。所以就定义了如果一个参数的估计量的数学期望是该参数的真值，则该估计量是无偏估计。
  • 无偏估计也意味着训练样本个数足够多，该估计值就是参数的真实值。因为我们只是取了部分样本来估计，当我们增加所取的样本，甚至到把整个样本集都拿来，那肯定是无偏估计。
  • 因此，分别计算均值和协方差的估计偏差，得到均值是无偏估计，协方差是有偏估计，而且随之训练样本的个数增大，偏差减小。即1/N，因此实际使用时，将估计值乘N/N-1。

3.6贝叶斯估计（1）

  • 网上查了资料，感觉这一节讲的是最大后验估计（MAP）。

  • 概率分布的参数θ作为随机变量，那么给定参数θ的先验概率和训练样本，估计参数θ分布的后验概率。

  • 假设，Ci类的观测似然概率是单维高斯分布，并且方差1已知，那么待估计参数θ就是均值1。并且假设θ的先验概率分布也服从单维高斯分布，方差2和均值2已知。因此可以计算后验概率。

  • 计算出来的后验概率也是高斯分布的形式，方差3和均值3和方差1、方差2，均值1、均值2还有样本个数有关。

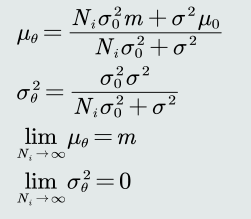
    image-20210501144331974

  • 当样本个数非常多的时候，可以观察到，方差3趋近于0，均值3就会是无偏估计。也就是逐渐逼近最大似然估计。

  • 如果方差2等于0，根据公式，可以看到均值3会等于均值2，也就是说先验概率的高斯分布均值决定了这个后验概率的高斯分布的均值，也就是说样本个数的多少已经对这个后验概率的高斯分布的均值没有影响了。

  • 如果方差2远大于方差1，那么均值3就会逼近于m，m也就是样本均值，这就说明了样本个数增多，会使得估计值逐渐逼近无偏估计。

  • 综上，说明了贝叶斯估计具有不断学习的能力，它可以在刚开始只有少数的样本进行学习，但随着样本个数的增加，逐渐学习到该参数期望的真值。

3.7贝叶斯估计（2）

  • 这一节就应该是贝叶斯估计了。

  • 利用上一节的θ的后验概率，再和θ是确定值的情况下的观测似然进行相乘并对θ进行积分，计算得到关于θ的边缘概率。从而得到观测似然概率的估计，该估计也是服从高斯分布的。

  • 并且随着样本个数的增加，这个高斯分布的均值逐渐趋于真值，方差逐渐趋于0，也就说明了贝叶斯估计的不断学习能力。这里方差趋于0，也就是他会变得越来越瘦、最后变成一个垂直X轴的直线，这也就说明了贝叶斯估计学习到了最优的值，非这个值不可了。

  • 对比最大似然估计，最大似然估计有明确的目标函数，只需要求偏导就能得到估计值。而贝叶斯估计有多个取值的可能性，在学习的过程中，逐渐缩小取值的范围，直到趋近真值，所以贝叶斯估计计算复杂度很高。

  • 这里再记录一下网上看到的博文和我的理解，讲MLE、MAP和贝叶斯估计的。

    1.MLE就好像是通过一个指标，来判断一系列待定的参数的好坏，并直接选取指标最好、最高的来解决问题。

    2.MAP就不仅仅通过指标了，还加入了一个参照，这个参照就是先验概率，然后计算后验概率，选取后验概率最高的参数来解决问题。

    3.贝叶斯估计继续优化，在得到的后验概率的基础上，与θ是确定值情况下的观测似然相乘，就好像是这里的高斯分布，在对应与不同的θ时，有不同的值，这个不同的值就是一个权重，与对应的θ的后验概率相乘，最后累加（也就是积分），得到一个值，这个值通过了重重计算和考验，所以很靠谱，用它来解决问题。

3.8无参数概率密度估计（1）&& 3.9直方图与核密度估计

  • 无参数估计方法：KNN估计、直方图估计、核密度估计

  • image-20210501152749307

  • image-20210501152803914