动态规划系列
70 爬楼梯
使用数组
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int climbStairs(int n) {
int dp[46];
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};不使用数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int climbStairs(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
if (n == 2) {
return 2;
}
int a;
int b = 1;
int c = 2;
for (int i = 3; i <= n; i++) {
a = b + c;
b = c;
c = a;
}
return c;
}
};
118 杨辉三角
直接模拟题目,注意 vector<vector
> ans(numRows); 的初始化 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans(numRows);
for (int i = 0; i < numRows; i++) {
ans[i].resize(i + 1);
ans[i][0] = 1;
ans[i][i] = 1;
for (int j = 1; j < i; j++) {
ans[i][j] = ans[i - 1][j - 1] + ans[i - 1][j];
}
}
return ans;
}
};
119 杨辉三角 II
使用两个数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> now;
vector<int> last;
for (int i = 0; i <= rowIndex; i++) {
now.resize(i + 1);
now[0] = 1;
now[i] = 1;
for (int j = 1; j < i; j++) {
now[j] = last[j] + last[j - 1];
}
last = now;
}
return now;
}
};使用一个数组(题解)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> now;
for (int i = 0; i <= rowIndex; i++) {
now.resize(i + 1);
now[0] = 1;
now[i] = 1;
// 倒着来,不会影响存储,正着会影响
for (int j = i - 1; j > 0; j--) {
now[j] += now[j - 1];
}
}
return now;
}
};使用组合式公式
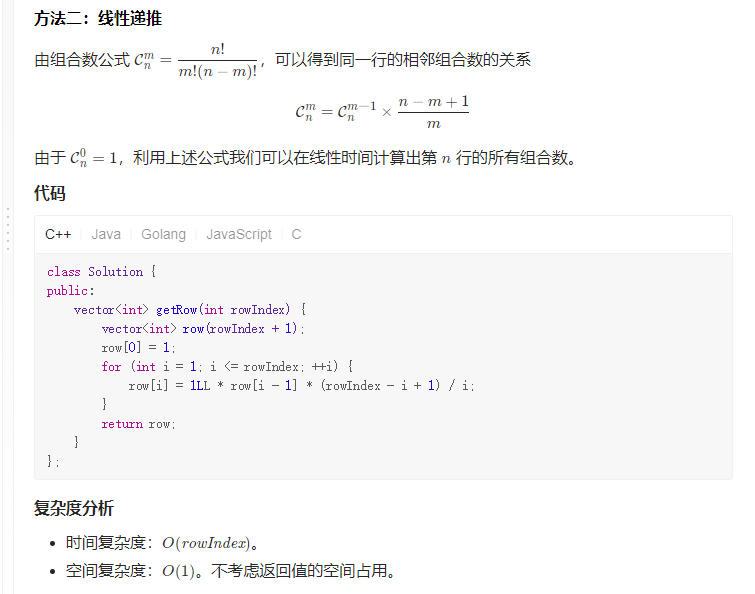
121 买卖股票的最佳时机
记录最大利润,更新最小指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int temp = prices[0];
for (int i = 1; i < prices.size(); i++) {
if (temp >= prices[i]) {
temp = prices[i];
} else {
ans = max(ans, prices[i] - temp);
}
}
return ans;
}
};
338 比特位计数
除2后判断最低为是奇数还是偶数
1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
vector<int> countBits(int n) {
vector<int> dp(n + 1);
dp[0] = 0;
for (int i = 1; i <= n; i++) {
dp[i] = dp[i >> 1] + (i & 1);
}
return dp;
}
};将最高位砍去然后直接加1
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
vector<int> countBits(int n) {
vector<int> bits(n + 1);
int highBit = 0;
for (int i = 1; i <= n; i++) {
if ((i & (i - 1)) == 0) {
highBit = i;
}
bits[i] = bits[i - highBit] + 1;
}
return bits;
}
};将该数减1然后&自己,然后加1
1
2
3
4
5
6
7
8
9
10class Solution {
public:
vector<int> countBits(int n) {
vector<int> bits(n + 1);
for (int i = 1; i <= n; i++) {
bits[i] = bits[i & (i - 1)] + 1;
}
return bits;
}
};
392 判断子序列
简单模拟,快慢指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
bool isSubsequence(string s, string t) {
int low = 0;
if (s == t && t.size() == 0) {
return true;
}
if (s.size() > t.size()) {
return false;
}
for (int i = 0; i < t.size(); i++) {
if (s[low] == t[i]) {
low++;
}
if (low == s.size()) {
return true;
}
}
return false;
}
};动态规划,记录了t中每一位上,所有下一个可能的字符的位置,对于大量输入的s,该方式能够提高效率
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
bool isSubsequence(string s, string t) {
// 需要预先加一个空字符串来防止'abc' -> 'abecf'为false的情况
t.insert(t.begin(), ' ');
vector<vector<int>> mat(t.size(), vector<int> (26, 0));
for (char c = 'a'; c <= 'z'; c++) {
int idx = -1;
for (int i = t.size() - 1; i >= 0; i--) {
mat[i][c - 'a'] = idx;
if (c == t[i]) {
idx = i;
}
}
}
int idx = 0;
for (int i = 0; i < s.size(); i++) {
if (mat[idx][s[i] - 'a'] == -1) {
return false;
}
idx = mat[idx][s[i] - 'a'];
}
return true;
}
};
509 斐波那契数
动态规划,使用滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int fib(int n) {
int a = 0;
int b = 1;
if (n == 0) {
return a;
}
if (n == 1) {
return b;
}
int c;
for (int i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return c;
}
};使用矩阵快速幂(该方式容易忘)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
int fib(int n) {
if (n < 2) {
return n;
}
vector<vector<int>> a{{1, 1}, {1, 0}};
vector<vector<int>> res;
res = mul_pow(a, n - 1);
return res[0][0];
}
vector<vector<int>> mul_pow(vector<vector<int>> a, int n) {
vector<vector<int>> res{{1, 0}, {0, 1}};
while (n) {
if (n & 1) {
res = mul_mat(res, a);
}
n >>= 1;
a = mul_mat(a, a);
}
return res;
}
vector<vector<int>> mul_mat(vector<vector<int>> a, vector<vector<int>> b) {
vector<vector<int>> res{{0, 0}, {0, 0}};
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
res[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
}
}
return res;
}
};通项公式,(通项公式需要复习一下)
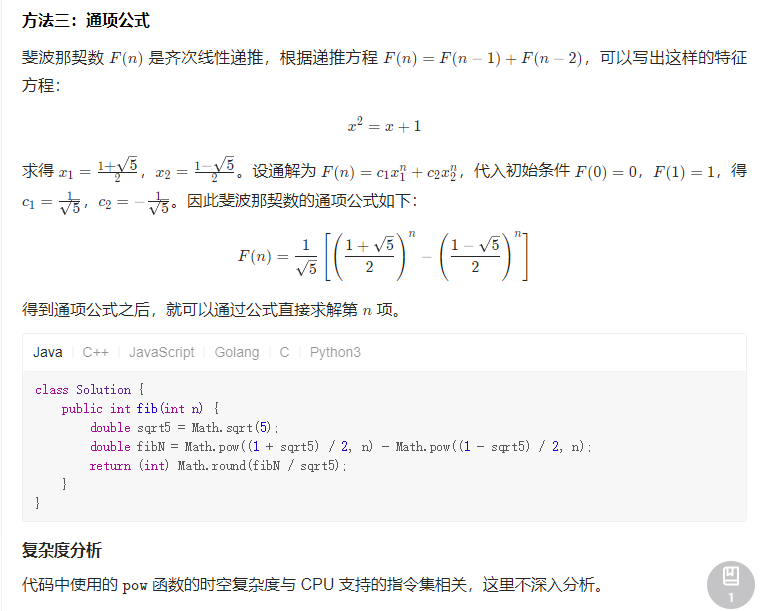
746 使用最小花费爬楼梯
动态规划,使用数组存储
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n + 1, 0);
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < n; i++) {
dp[i] = cost[i] + min(dp[i - 1], dp[i - 2]);
}
return min(dp[n - 1], dp[n - 2]);
}
};动态规划,使用滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
int a = cost[0];
int b = cost[1];
int c;
for (int i = 2; i < n; i++) {
c = cost[i] + min(a, b);
a = b;
b = c;
}
return min(a, b);
}
};
1025 除数博弈
动态规划,判断之前是否是必输态
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool divisorGame(int n) {
vector<int> dp (n + 2);
dp[1] = false;
dp[2] = true;
for (int i = 3; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (i % j == 0 && dp[i - j] == 0) {
dp[i] = true;
break;
}
}
}
return dp[n];
}
};直接找规律
1
2
3
4
5
6class Solution {
public:
bool divisorGame(int n) {
return n % 2 == 0;
}
};
1137 第N个泰波那契数
直接滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int tribonacci(int n) {
if (n < 2) {
return n;
}
if (n == 2) {
return 1;
}
int a = 0;
int b = 1;
int c = 1;
int d;
for (int i = 3; i <= n; i++) {
d = a + b + c;
a = b;
b = c;
c = d;
}
return d;
}
};
1646 获取生成数组中的最大值
直接模拟,需要一个dp数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int getMaximumGenerated(int n) {
if (n < 2) {
return n;
}
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
int res = 1;
for (int i = 2; i <= n; i++) {
if (i % 2) {
dp[i] = dp[i / 2] + dp[i / 2 + 1];
res = max(res, dp[i]);
} else {
dp[i] = dp[i / 2];
res = max(res, dp[i]);
}
}
return res;
}
};用了dfs,但是超时了,感觉思路是对的,题解也只有上面的做法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
int getMaximumGenerated(int n) {
if (n < 2) {
return n;
}
int k = n - 1;
if (n % 2) {
k = n;
}
return dfs(k);
}
int dfs(int n) {
if (n == 1) {
return 1;
}
if (n == 2) {
return 1;
}
int res;
if (n % 2) {
int a = n / 2;
int b = n / 2 + 1;
res = dfs(a) + dfs(b);
} else {
res = dfs(n);
}
return res;
}
};
LCP 07 传递信息
dfs,开了n * n的二维
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
int ans = 0;
int numWays(int n, vector<vector<int>>& relation, int k) {
vector<vector<int>> mp(n, vector<int> (n));
for (int i = 0; i < relation.size(); i++) {
int a = relation[i][0];
int b = relation[i][1];
mp[a][b] = 1;
}
dfs(0, k, n, mp);
return ans;
}
void dfs(int row, int step, int n, vector<vector<int>> mp) {
if (step < 0) {
return;
}
for (int i = 0; i < n; i++) {
if (mp[row][i]) {
if (step == 1 && i == n - 1) {
ans++;
return ;
}
dfs(i, step - 1, n, mp);
}
}
}
};dfs, 节省空间,不用n * n的二维,改为n * m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
int ans = 0;
int numWays(int n, vector<vector<int>>& relation, int k) {
vector<vector<int>> mp(n);
for (int i = 0; i < relation.size(); i++) {
int a = relation[i][0];
int b = relation[i][1];
mp[a].push_back(b);
}
dfs(0, k, n, mp);
return ans;
}
void dfs(int row, int step, int n, vector<vector<int>> mp) {
if (step < 0) {
return;
}
for (int i = 0; i < mp[row].size(); i++) {
if (step == 1 && mp[row][i] == n - 1) {
ans++;
return;
}
dfs(mp[row][i], step - 1, n, mp);
}
}
};bfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54class Solution {
public:
int ans = 0;
int numWays(int n, vector<vector<int>>& relation, int k) {
vector<vector<int>> mp(n);
for (int i = 0; i < relation.size(); i++) {
int a = relation[i][0];
int b = relation[i][1];
mp[a].push_back(b);
}
// dfs(0, k, n, mp);
ans = bfs(k, n, mp);
return ans;
}
void dfs(int row, int step, int n, vector<vector<int>> mp) {
if (step < 0) {
return;
}
for (int i = 0; i < mp[row].size(); i++) {
if (step == 1 && mp[row][i] == n - 1) {
ans++;
return;
}
dfs(mp[row][i], step - 1, n, mp);
}
}
int bfs(int step, int n, vector<vector<int>> mp) {
queue<int> q;
q.push(0);
for (int i = 0; i < step; i++) {
int qsize = q.size();
while (qsize) {
int temp = q.front();
q.pop();
for (int j = 0; j < mp[temp].size(); j++) {
q.push(mp[temp][j]);
}
qsize--;
}
}
int ans = 0;
while (q.size()) {
if (q.front() == n - 1) {
ans++;
}
q.pop();
}
return ans;
}
};动态规划,使用滚动数组,不断刷新迭代到该点的次数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int numWays(int n, vector<vector<int>>& relation, int k) {
vector<int> last(n, 0);
last[0] = 1;
for (int i = 0; i < k; i++) {
vector<int> now(n);
for (int j = 0; j < relation.size(); j++) {
int src = relation[j][0];
int dst = relation[j][1];
now[dst] += last[src];
}
last = now;
}
return last[n - 1];
}
};
LCS 01 下载插件
贪心,找规律,一直×2肯定是最优的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int leastMinutes(int n) {
if (n == 1) {
return n;
}
int ans;
int time = 0;
while (true) {
int a = pow(2, time);
int b = pow(2, time + 1);
if (a < n and n <= b) {
ans = time + 2;
break;
} else {
time++;
}
}
return ans;
}
};动态规划,时间空间都不够好
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
int leastMinutes(int n) {
vector<int> dp(n + 1);
dp[1] = 1;
for (int i = 2; i <= n; i++) {
// i + 1是因为3由2 * 2得,不由1 * 2得
dp[i] = min(dp[i - 1] + 1, dp[(i + 1) / 2] + 1);
}
return dp[n];
}
};
剑指offer 10-1 斐波那契数列
动态规划,直接在原题得基础上做取余操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int fib(int n) {
int a = 0;
int b = 1;
int m = 1000000007;
if (n < 2) {
return n;
}
int c;
for (int i = 2; i <= n; i++) {
c = (a + b) % m;
a = b % m;
b = c % m;
}
return c;
}
};矩阵快速幂,中间的乘法容易越界,需要用long
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
int m = 1000000007;
int fib(int n) {
if (n < 2) {
return n;
}
vector<vector<long>> a{{1, 1}, {1, 0}};
vector<vector<long>> res;
res = mul_pow(a, n - 1);
return res[0][0];
}
vector<vector<long>> mul_pow(vector<vector<long>> a, int n) {
vector<vector<long>> res = {{1, 0}, {0, 1}};
while (n) {
if (n & 1) {
res = mul_mat(res, a);
}
n >>= 1;
a = mul_mat(a, a);
}
return res;
}
vector<vector<long>> mul_mat(vector<vector<long>> a, vector<vector<long>> b) {
vector<vector<long>> res = {{0, 0}, {0, 0}};
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
res[i][j] = ((a[i][0] * b [0][j]) % m + (a[i][1] * b[1][j]) % m) % m;
}
}
return res;
}
};
剑指 Offer 10- II. 青蛙跳台阶问题
直接滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int numWays(int n) {
if (n == 0) {
return 1;
}
if (1 <= n and n <= 2) {
return n;
}
int a = 1;
int b = 2;
int c;
for (int i = 3; i <= n; i++) {
c = (a + b) % 1000000007;
a = b;
b = c;
}
return b;
}
};
剑指 Offer 42. 连续子数组的最大和
直接模拟,动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ans = nums[0];
int temp = nums[0];
for (int i = 1; i < nums.size(); i++) {
if (temp < 0) {
temp = nums[i];
} else {
temp += nums[i];
}
ans = max(ans, temp);
}
return ans;
}
};分治
面试题 08.01. 三步问题
动态规划模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int waysToStep(int n) {
int a = 1;
int b = 2;
int c = 4;
if (n == 1) {
return a;
}
if (n == 2) {
return b;
}
if (n == 3) {
return c;
}
int d;
for (int i = 4; i <= n; i++) {
d = ((a + b) % 1000000007 + c) % 1000000007;
a = b;
b = c;
c = d;
}
return d;
}
};
面试题 05.03. 翻转数位
使用了数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int reverseBits(int num) {
vector<int> temp;
int count = 0;
for (int i = 0; i < 32; i++) {
if (num & 1) {
count++;
} else {
temp.push_back(count);
count = 0;
}
num >>= 1;
}
temp.push_back(count);
if (temp.size() == 1) {
return temp[0];
}
int ans = 0;
for (int i = 0; i < temp.size() - 1; i++) {
ans = max(ans, temp[i] + temp[i + 1] + 1);
}
return ans;
}
};不用数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int reverseBits(int num) {
int last = 0;
int cur = 0;
int ans = 0;
for (int i = 0; i < 32; i++) {
if (num & 1) {
cur++;
} else {
ans = max(ans, last + cur);
last = cur + 1;
cur = 0;
}
num >>= 1;
}
return max(ans, last + cur);
}
};
面试题 17.16. 按摩师
直接模拟,动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int massage(vector<int>& nums) {
vector<int> dp(nums.size() + 1);
if (nums.size() == 0) {
return 0;
}
if (nums.size() == 1) {
return nums[0];
}
if (nums.size() == 2) {
return max(nums[0], nums[1]);
}
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.size() - 1];
}
};滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int massage(vector<int>& nums) {
if (nums.size() == 0) {
return 0;
}
if (nums.size() == 1) {
return nums[0];
}
if (nums.size() == 2) {
return max(nums[0], nums[1]);
}
int a = nums[0];
int b = max(nums[0], nums[1]);
int c;
for (int i = 2; i < nums.size(); i++) {
c = max(a + nums[i], b);
a = b;
b = c;
}
return c;
}
};
回溯系列
257 二叉树的所有路径
dfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> ans;
vector<string> binaryTreePaths(TreeNode* root) {
string s = "";
dfs(root, s);
return ans;
}
void dfs(TreeNode *node, string s) {
if (node == NULL) {
return ;
}
s += to_string(node -> val);
if (node -> left == NULL and node -> right == NULL) {
ans.push_back(s);
}
s += "->";
dfs(node -> left, s);
dfs(node -> right, s);
}
};bfs,需要同时记录path路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> ans;
vector<string> binaryTreePaths(TreeNode* root) {
string s = "";
// dfs(root, s);
bfs(root);
return ans;
}
void dfs(TreeNode *node, string s) {
if (node == NULL) {
return ;
}
s += to_string(node -> val);
if (node -> left == NULL and node -> right == NULL) {
ans.push_back(s);
}
s += "->";
dfs(node -> left, s);
dfs(node -> right, s);
}
void bfs(TreeNode *node) {
queue<TreeNode*> q;
queue<string> path;
q.push(node);
path.push(to_string(node -> val));
while (q.size()) {
TreeNode* t = q.front();
string s = path.front();
q.pop();
path.pop();
if (t -> left == NULL and t -> right == NULL) {
ans.push_back(s);
}
if (t -> left) {
q.push(t -> left);
path.push(s + "->" + to_string(t -> left ->val));
}
if (t -> right) {
q.push(t -> right);
path.push(s + "->" + to_string(t -> right ->val));
}
}
}
};
401 二进制手表
时分枚举
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
vector<string> readBinaryWatch(int turnedOn) {
vector<string> ans;
for (int i = 0; i < 12; i++) {
for (int j = 0; j < 60; j++) {
if (__builtin_popcount(i) + __builtin_popcount(j) == turnedOn) {
ans.push_back(to_string(i) + ':' + (j < 10 ? '0' + to_string(j) : to_string(j)));
}
}
}
return ans;
}
};二进制枚举
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<string> readBinaryWatch(int turnedOn) {
vector<string> ans;
// for (int i = 0; i < 12; i++) {
// for (int j = 0; j < 60; j++) {
// if (__builtin_popcount(i) + __builtin_popcount(j) == turnedOn) {
// ans.push_back(to_string(i) + ':' + (j < 10 ? '0' + to_string(j) : to_string(j)));
// }
// }
// }
for (int i = 0; i < 1024; i++) {
int h = i >> 6;
int m = i & 63;
if (h < 12 and m <= 59 and __builtin_popcount(i) == turnedOn) {
ans.push_back(to_string(h) + ':' + (m < 10 ? '0' + to_string(m) : to_string(m)));
}
}
return ans;
}
};回溯
1
随机刷到
1422 分割字符串的最大得分
模拟,使用了数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int maxScore(string s) {
vector<int> temp;
int sum = 0;
for (int i = 0; i < s.size(); i++) {
sum += (s[i] - '0');
temp.push_back(sum);
}
int res = 0;
int ans;
for (int i = 0; i < temp.size() - 1; i++) {
ans = (i + 1 - temp[i]) + (sum - temp[i]);
res = max(ans, res);
}
return res;
}
};不使用数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int maxScore(string s) {
int score = 0;
if (s[0] == '0') {
score++;
}
for (int i = 1; i < s.size(); i++) {
if (s[i] == '1') {
score++;
}
}
int ans = score;
for (int i = 1; i < s.size() - 1; i++) {
if (s[i] == '0') {
score++;
} else {
score--;
}
ans = max(ans, score);
}
return ans;
}
};